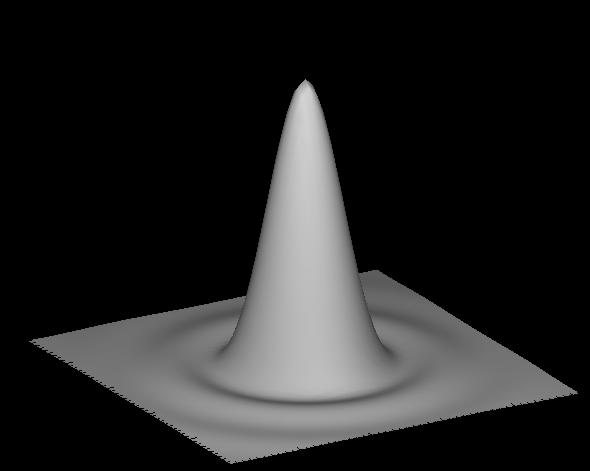
 Форма изображения точечного
источника (звезды) в идеальном телескопе в
отсутствии
Форма изображения точечного
источника (звезды) в идеальном телескопе в
отсутствииатмосферы определяется дифракцией и описывается функцией Эйри:
Назад: Введение
Вперед: Деформируемые
зеркала
 Форма изображения точечного
источника (звезды) в идеальном телескопе в
отсутствии
Форма изображения точечного
источника (звезды) в идеальном телескопе в
отсутствии
атмосферы определяется дифракцией и описывается
функцией Эйри:
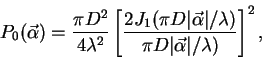 |
(1) |
где:
Первое темное кольцо находится на угловом
расстоянии ![]() от центра. Эта величина
от центра. Эта величина
часто принимается как мера разрешения
идеального телескопа.
Изображение ![]() астрономического объектаt
астрономического объектаt ![]() может рассматриваться как множество
может рассматриваться как множество
точек, каждая из которых представлена функцией
Эйри. Это может быть
записано в виде свертки:
| (2) |
Мы называем это соотношение уравнением
изображения. Изображение по сравнению
с объектом сглажено, и его разрешение снижено.
Однако, для данного диаметра телескопа
это снижение наименее возможное. Говорят, что
изображение в данном случае ограничено
дифракцией . Пример астрономического
изображения (центра Галактики)
с различным разрешением дано ниже.
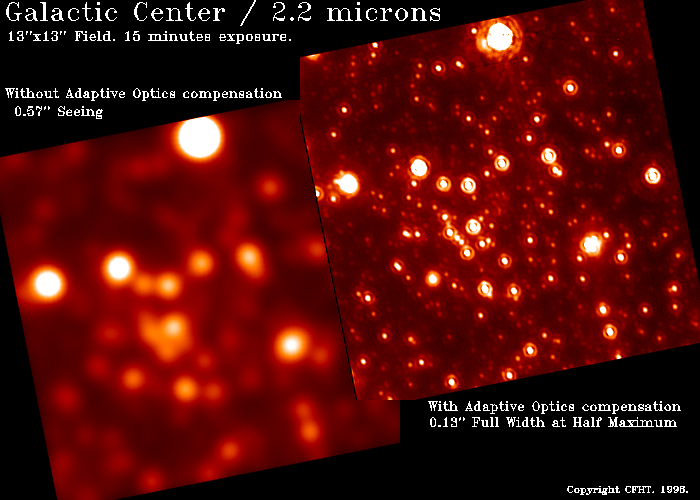 |
| Центр Галактики. (Длина волны 2,2 мкм, поле зрения 13х13 угл. секунд, экспозиция 15 мин. Слева: без АО компенсации, качество изображения 0,57 угл.сек. Справа: с АО компенсацией, ширина на половине высоты 0,19 угл.сек. |
Вопрос: Как зависит от длины волны разрешение, ограниченное дифракцией?
Вопрос: Вычислите разрешение человеческого глаза, ограниченное дифракцией.
Что случается, если телескоп неидеальный?
Изображение становится не таким хорошим, как
определенное
функцией Эйри, разрешение ухудшается ещё больше.
Но уравнение изображения остается справедливым!
Таким образом, функции рассеяния точки (ФРТ)
достаточно для того, чтобы характеризовать
изображение.
Ширина ФРТ есть мера разрешения.
Примечание 1. Безусловно, мы предполагаем в
уравнениях, что ![]() является изображением звезды
является изображением звезды
с единичной интенсивностью, т.е. интеграл от
![]() по
по
![]() равен 1. Таким образом, уравнение изображения
равен 1. Таким образом, уравнение изображения
сохраняет общий световой поток астрономического
объекта и только перераспределяет его различным
образом между пикселями.
Примечание 2. Мы предполагаем, что ФРТ
имеет одинаковую форму по всему полю зрения.
Это условие
называется изопланатизмом. Это не всегда
справедливо для астрономических изображений, в
частности,
в адаптивной оптике, т.к. ФРТ медленно меняется
по полю. В этом случае уравнение изображения
может
быть применено к части поля зрения..
Форма ФРТ может быть неправильной, какая
числовая оценка разрешения
используется в этом случае?
1. FWHM - полная ширина ФРТ на половине высоты .
2. Коэффициент Штреля ![]() ,
т.е. интенсивность в центре ФРТ , деленная
,
т.е. интенсивность в центре ФРТ , деленная
на интенсивность в центре функции Эйри. Чем выше
коэффициент Штреля, тем лучше
разрешение. Изображение, ограниченное
диффракцией, лучше всего. Следовательно
всегда![]() .
.
3. Эффективная энергия. По определению,
интеграл от ФРТ равен 1. Интеграл ФРТ
по кругу радиуса![]() называется эффективной энергией. Эта величина
важна при
называется эффективной энергией. Эта величина
важна при
наблюдении слабых объектов, когда нужно собрать
как можно больше фотонов.
Пример ФРТ с компенсацией турбулентности дан
на рисунке ниже.
.
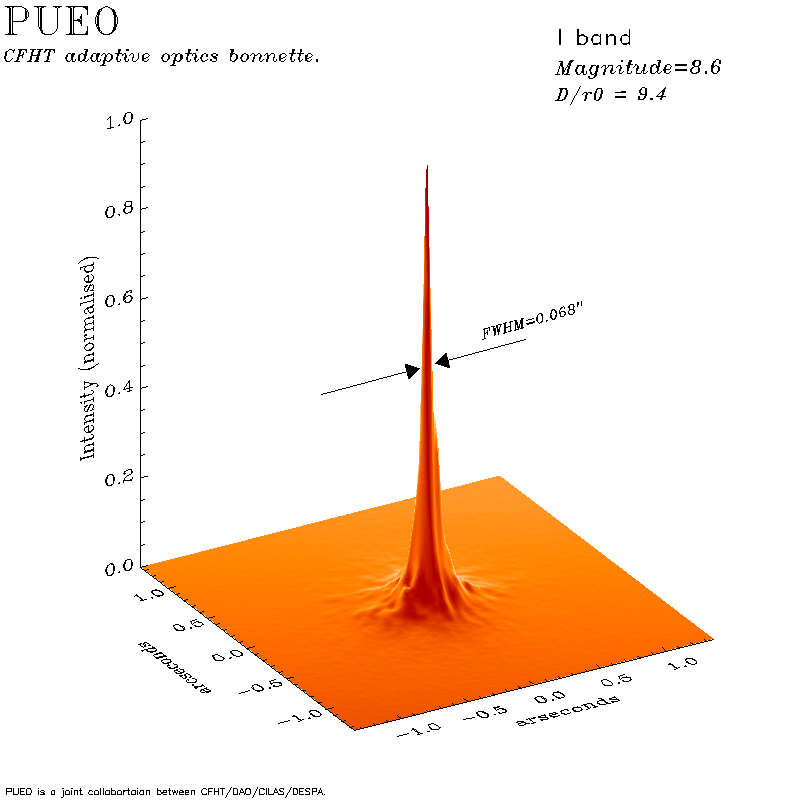 |
| Подпись под рисунком. I band - диапазон
спектра, Magnitude - звездная величина, intensity (normalised) - интенсивность (нормированная), arcsecond - угловые секунды. |
Вопрос: Предположим, что ФРТ
в два раза уже, насколько изменится
коэффициент Штреля?
Вопрос: Что станет с
коэффициентом Штреля, если половина объектива
телескопа
(идеального) дает фазовый сдвиг ![]() ?
?
Другой способ рассмотрения уравнения
изображения состоит в использовании
преобразования Фурье (ПФ , мы обозначаем его
тильдой). Свертка превращается
в произведение, так что
| (3) |
Здесь ![]() - пространственная частота ( если
- пространственная частота ( если ![]() iизмеряется в радианах, то
iизмеряется в радианах, то ![]() измеряется в обратных радианах или циклах на
радиан).
измеряется в обратных радианах или циклах на
радиан).
![]() называется оптической передаточной функцией
(ОПФ). Она
называется оптической передаточной функцией
(ОПФ). Она
описывает изменение модуля и фазы
преобразования Фурье объекта в процессе образования
изображения. Модуль ОПФ называется
модуляционной передаточной функцией (МПФ).
Для астрономических (некогерентных) изображений
.![]() .
Как правило, МПФ уменьшается с ростом
частот, следовательно, мелкие (высокочастотные)
детали изображения ослабляются и, в конечном
счете,
утрачиваются.
.
Как правило, МПФ уменьшается с ростом
частот, следовательно, мелкие (высокочастотные)
детали изображения ослабляются и, в конечном
счете,
утрачиваются.
Известно, что для любой оптической системы ![]() при
при ![]() , где
, где ![]() называется
называется
частотой среза, а ![]() -
максимальный размер апертуры. Это означает, что
информация при пространственных
-
максимальный размер апертуры. Это означает, что
информация при пространственных
частотах выше ![]() безвозвратно потеряна. Чем меньше объекты,
которые мы хотим наблюдать, тем
безвозвратно потеряна. Чем меньше объекты,
которые мы хотим наблюдать, тем
больше должен быть телескоп!
ФРТ и ОПФ связаны через преобразование Фурье,
поэтому, если известно одно, то известно другое,
т.е. это одно и то же , описанное различными
способами. Из свойств фурье-преобразования
следует,
что ![]() (нормировка ФРТ), а коэффициент Штреля
пропорционален интегралу ОПФ по частоте.
(нормировка ФРТ), а коэффициент Штреля
пропорционален интегралу ОПФ по частоте.
Вопрос: Каков минимальный
размер телескопа, необходимого, чтобы различить
на удалении 5 км
доски забора с расстоянием 10 см ?
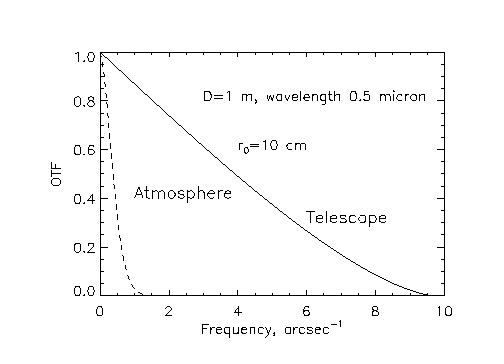 Атмосферная турбулентность может
рассматриваться как случайные фазовые
аберрации, добавляемые
Атмосферная турбулентность может
рассматриваться как случайные фазовые
аберрации, добавляемые
к аберрациям телескопа. Эти аберрации постоянно
изменяются со временем, соответственно
изменяется ФРТ. Здесь мы рассматриваем среднюю
ФРТ, что соответствует случаю больших времен
экспозиции. Теория приводит к выражению
| (4) |
Здесь ![]() - ОПФ телескопа (см. ранее) и
- ОПФ телескопа (см. ранее) и ![]() атмосферная передаточная
функция. Для больших
атмосферная передаточная
функция. Для больших
телескопов с хорошим оптическим качеством
разрешение полностью определено атмосферой,
поэтому мы пренебрежем первым членом![]() .
Конечно, атмосферная ФРТ
.
Конечно, атмосферная ФРТ
получается из ![]() с помощью Фурье-преобразования.
с помощью Фурье-преобразования.![]() .
.
Атмосферная ОПФ связана со статистикой фазовых
аберраций атмосферы так называемой
фазовой структурной функцией ![]() (см. следующий раздел)::
(см. следующий раздел)::
| (5) |
Примечание: в этой формуле мы переходим от пространственных координат в плоскости волнового фронта к пространственным частотам в плоскости изображений, умноженным на длину волны. Это соотношение следует из волновой оптики: каждая фурье-компонента изображения образуется интерференцией световых волн отделенных определенным расстоянием. Этот принцип используется в радио- и оптических интерферометрах.
Вопрос: Предположим, что
форма атмосферной ФРТ Гауссова. Какова форма
структурной
функции?
Вопрос: Чувствительна ли
форма атмосферной ФРТ к структурной функции в
областях, где ![]() и
и ![]() ?
?
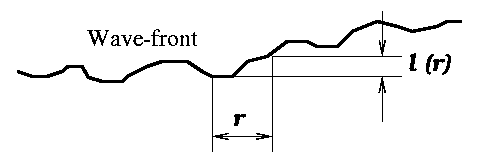
Возмущенный атмосферой волновой фронт может
быть представлен как смятый лист бумаги.
Волна, приходящая от звезды, до входа в атмосферу
плоская. Затем некоторая её часть проходит через
воздух, более теплый (и имеющий меньший
показатель преломления) и приходит раньше,
другие части волны замедляются и задерживаются.
Таким образом,
волновой фронт деформируется. Целью Адаптивной
оптики является компенсация этих искажений. Но
сначала нужно описать их в
статистическом смысле.
Воздух обладает некоторой дисперсией, но
обычно этим пренебрегают и считают возмущения
длины оптического пути ![]() ахроматичными
ахроматичными
(не зависящими от длины волны). Однако, фаза
оптической волны ![]() сильно зависит от длины волны
сильно зависит от длины волны ![]() !
Говоря о возмущениях, мы полагаем, что их среднее
значение равно нулю
!
Говоря о возмущениях, мы полагаем, что их среднее
значение равно нулю ![]() (угловые скобки означают статистическое
усреднение)..
(угловые скобки означают статистическое
усреднение)..
Хотя случайные процессы, подобные![]() обычно описываются функциями
корреляции или ковариации, в науке об атмосфере
предпочтительны структурные функции.
Структурная функция - это средний квадрат разности между двумя значениями случайного процесса:
обычно описываются функциями
корреляции или ковариации, в науке об атмосфере
предпочтительны структурные функции.
Структурная функция - это средний квадрат разности между двумя значениями случайного процесса:
| (6) |
Вопрос: Как связаны между
собой структурная функция и функция ковариации ![]() ?
?
Вопрос: Как структурная
функция атмосферы ![]() зависит от длины волны
зависит от длины волны ![]() ?
?
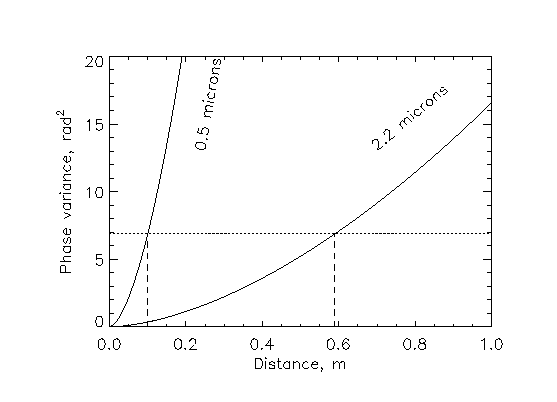 Модель Колмогорова атмосферных
искажений предписывает определенную форму
фазовой структурной функции , а именно:
Модель Колмогорова атмосферных
искажений предписывает определенную форму
фазовой структурной функции , а именно:
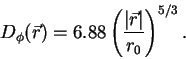 |
(7) |
Эта формула содержит только один параметр, ![]() , который называется радиусом
когерентности
, который называется радиусом
когерентности
атмосферы или параметром Фрида. Из того
факта, что длина пути ахроматична, немедленно
следует, чтоt ![]() .
Когда указываете
.
Когда указываете ![]() ,
всегда оговаривайте соответствующую длину
волны!
,
всегда оговаривайте соответствующую длину
волны!
Описанная модель, хотя она может выглядеть
примитивной, является фундаментом целой теории создания изображений через турбулентную среду, включая
адаптивную оптику. Конечно, при больших
расстояниях
(более нескольких метров) и малых (менее 1 см)
модель не действует, но это оказывается не очень
важным.
Вопрос: Какова величина
среднего квадратического значения разности фаз
в атмосфере на расстоянии
.![]() в радианах и длинах волн?
в радианах и длинах волн?
Вопрос: Если ![]() см при длине волны 0.5 микрон, какова величина
см при длине волны 0.5 микрон, какова величина ![]() на длине
на длине
волны 2.2 микрона?
Подставим эту модель в атмосферную ОПФ и
получим её в виде:
| (8) |
Атмосферная ОПФ при более длительных экспозициях
получается путем применения к этому уравнению
преобразования Фурье.
Численное вычисление дает соотношение между
полной шириной на половине высоты атмосферной
ФРТ ( называемой ![]() ,
или качество изображения) и
,
или качество изображения) и ![]() :
:
| (9) |
На длине волны 0.5 микрон качество изображения в 1 угловую
секунду соответствует ![]() =10.1
cm.
=10.1
cm.
Число Штреля атмосферной ФРТ в точности такое
же, как у идеального телескопа диаметра ![]() (это причина,
(это причина,
по которой появился странный коэффициент 6,88).
Поскольку для больших телескопов![]() , коэффициент Штреля
, коэффициент Штреля
просто . ![]() .
.
Вопрос: Чему равен
коэффициент Штреля для изображений 4-х метрового
телескопа при больших экспозициях
при качестве изображения 1 угловая секунда на длинах волн 0.5 и
2.2 микрон?
Радиус Фрида ![]() иногда
отождествляют с характерным масштабом
атмосферных возмущений. Это не совсем правильно:
иногда
отождествляют с характерным масштабом
атмосферных возмущений. Это не совсем правильно:
мы видим, что закон Колмогорова не имеет
характеристического масштаба. Однако, только
возмущения, имеющие
размер такого же порядка, как ![]() существенны для построения изображения при
больших экспозициях.
существенны для построения изображения при
больших экспозициях.
При меньших размерах искажения много меньше ![]() , при больших
, при больших ![]() становится так велик, что
становится так велик, что
падает до нуля атмосферная ОПФ.
Локально величина турбулентных флуктуаций
показателя преломления в воздухе описывается структурной
постоянной
показателя преломления ![]() который измеряется в странных единицах, m
который измеряется в странных единицах, m![]() . Зависимость
. Зависимость ![]() от высоты называется профилем
турбулентности. Качество изображения зависит от суммарного
влияния всех слоёв атмосферы.
от высоты называется профилем
турбулентности. Качество изображения зависит от суммарного
влияния всех слоёв атмосферы.
| (10) |
где ![]() - высота,
- высота, ![]() -
зенитный угол и интегрирование производится от
телескопа до максимальной
-
зенитный угол и интегрирование производится от
телескопа до максимальной
высоты турбулентности (что-то около 20 км).
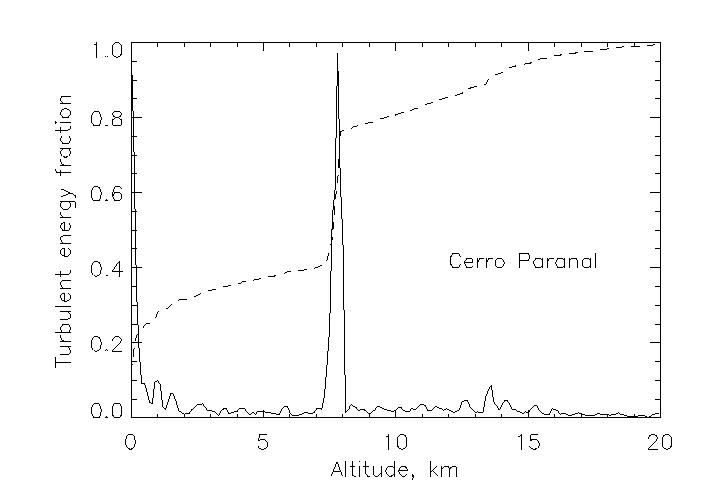 .
.
Пояснения к рисунку:
Turbulent energy fraction - Доля энергии турбулентности
Altitude, km - Высота, км
На этом графике показан пример профиля
турбулентности над горой Серро Паранал (Чили), на
которой расположена
Южная европейская обсерватория (ESO), в
относительных единицах (сплошная линия).
Отношение энергии
турбулентности к данной высоте показана
штриховой линией. Хотя в этом случае
значительная часть турбулентности
была сосредоточена только в двух слоях, однако
около 1/3 общей энергии распределено по всем
высотам.
Вопрос: Из этого
соотношения найдите как ![]() и
качество изображения зависят от зенитного угла.
и
качество изображения зависят от зенитного угла. ![]() .
.
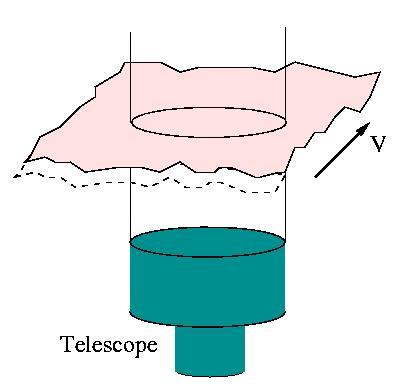 Турбулентность часто может быть смоделирована
как закрепленные фазовые экраны, которые
двигаются ветром перед
Турбулентность часто может быть смоделирована
как закрепленные фазовые экраны, которые
двигаются ветром перед
телескопом. Зная пространственные свойства
фазовых экранов (структурные функции) и
скорость ветра, мы знаем
также временное поведение возмущений. Постоянная
времени атмосферы ![]() определяется как
определяется как
| (11) |
где ![]() - скорость ветра,
усредненная по высоте. Параметр
- скорость ветра,
усредненная по высоте. Параметр ![]() определяет, насколько быстродействующей
определяет, насколько быстродействующей
должна быть нужная адаптивная система.
Вопрос: Считая типичным
значение ![]() =20
m/s, каким была бы постоянная времени атмосферы на
длинах волн
=20
m/s, каким была бы постоянная времени атмосферы на
длинах волн
0.5 и 2.2 микрон при качестве изображения 1 угловая
секунда?
Изображения астрономических объектов
полученные с временем экспозиции ![]() или короче называются
или короче называются
короткоэкспозиционными. Они соответствуют
зафиксированным (замороженным) атмосферным
аберрациям.
При больших временах экспозиции аберрации
усредняются, и при экспозициях, много больших ![]() получается
получается
ОПФ с большой экспозицией.
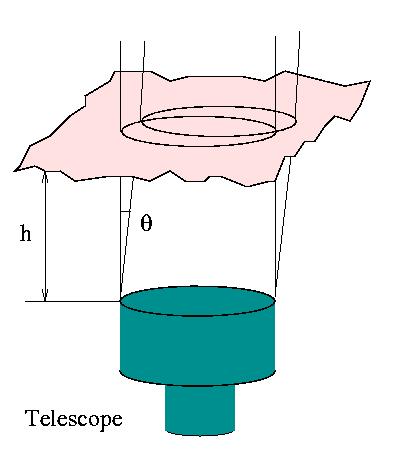 Атмосферная ФРТ при
длительных экспозициях не зависит от
направления наблюдения (изопланатична), потому, что турбулентность и её структурная функция статистически одинаковы по всему полю. Но мгновенные атмосферные фазовые аберрации зависят от направления: пучок лучей
телескопа, направленный на атмосферный слой
толщиной 10 км сдвинут
Атмосферная ФРТ при
длительных экспозициях не зависит от
направления наблюдения (изопланатична), потому, что турбулентность и её структурная функция статистически одинаковы по всему полю. Но мгновенные атмосферные фазовые аберрации зависят от направления: пучок лучей
телескопа, направленный на атмосферный слой
толщиной 10 км сдвинут
на 0.5 м при угловом смещении 10 угловых секунд.
Принятое определение угла атмосферного
изопланатизма ![]() :
:
| (12) |
где ![]() некоторая высота характеризующая среднюю
турбулентность. Усреднение выполняется по
профилю
некоторая высота характеризующая среднюю
турбулентность. Усреднение выполняется по
профилю
![]() с весовым коэффициентом
с весовым коэффициентом ![]() , Для характерных условий
получается сравнительно большая величина
, Для характерных условий
получается сравнительно большая величина ![]() .
.
Вопрос: Каков угол
изопланатизма
![]() на длинах волн 0.5 и 2.2. мкм при
качестве изображения 1 угловая секунда?
на длинах волн 0.5 и 2.2. мкм при
качестве изображения 1 угловая секунда?
Это явление очень вредно в адаптивной оптике,
потому, что ограничивает расстояние между
опорной звездой и
исследуемым объектом. Оказывается, что для
большинства объектов нет подходящих (ярких и
близко расположенных)
опорных звезд, поэтому требуются искусственные
лазерные опорные звезды. С другой стороны, для увеличения корректируемого поля может быть предложена трёхмерная коррекция турбулентности ( много-контурная адаптивная оптика - МСАО).
В оптике аберрации часто представляютя в виде
суммы специальных полиномов, называемых полиномами
Цернике.
Случайные атмосферные аберрации могут быть
рассмотрены таким же способом, однако,
коэффициенты таких деформаций
(дефокусировка, астигматизм, т.д.) в этом случае
являются случайными функциями, изменяющимися во
времени.
Полином Цернике ![]() определен в полярных координатах
определен в полярных координатах ![]() на круге единичного радиуса
на круге единичного радиуса ![]() . Они
. Они
характеризуются радиальным порядком ![]() и азимутальным порядком
и азимутальным порядком ![]() (для данного
(для данного ![]() ,
, ![]() принимает
принимает
значения от 0 до ![]() ). ).
Часто. вместо двух индексов
). ).
Часто. вместо двух индексов ![]() и
и ![]() используется сквозная нумерация с
единственным индексом
используется сквозная нумерация с
единственным индексом ![]() . Для каждого данного радиального порядка
. Для каждого данного радиального порядка![]() , существуют всего
, существуют всего ![]() полиномов Цернике..
полиномов Цернике..
Первые моды Цернике называются как общепринятые аберрации и имеют простой смысл (см. Таблицу первых 15 мод Цернике).
Польза мод Цернике состоит в том, что они
ортогональны, т.е. скалярное произведение ![]() равно 1, если
равно 1, если ![]() ,
и 0 во всех других случаях.
,
и 0 во всех других случаях.
Скалярное произведение определяется как
интеграл по апертуре телескопа:
| (13) |
Теперь любоая фазовая аберрация ![]() внутри зрачка телескопа может
быть представлена как бесконечная
внутри зрачка телескопа может
быть представлена как бесконечная
сумма полиномов Цернике.
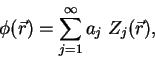 |
(14) |
и коэффициенты находятся как скалярные произведения:
| (15) |
Часто ограниченное количество мод Цернике уже
дает достаточно хорошее представление
атмосферных аберраций.
Если эти моды корректируются адаптивной оптикой,
достигается качество изображения,почти равное
дифракционному.
Поршневая мода соответствует постоянной фазе,
которая не влияет на качество изображения.
Обычно поршневой
модой пренебрегают.
Вопрос: 4-х-метровый
телескоп, относительное отверстие, ![]() , расфокусирован на 1
мм. Вычислите результирующую
, расфокусирован на 1
мм. Вычислите результирующую
аберрацию . ![]() для длин волн 0.5 и 2.2 мкм
для длин волн 0.5 и 2.2 мкм
Вопрос: Предположим,
атмосферная аберрация содержит только наклоны
по двум осям с равными амплитудами ![]() .
Напишите соответствующую фазовую структурную
функцию.
.
Напишите соответствующую фазовую структурную
функцию.
Ортогональность мод Цернике дает простой
способ вычисления фазовой вариации
интегрированной по зрачку. Для одной
моды это ![]() .
Вариация по всем модам равна сумме квадратов
коэффициентов, начиная со второго (поршень
.
Вариация по всем модам равна сумме квадратов
коэффициентов, начиная со второго (поршень
исключается).
Используя данную модель турбулентности
Колмогорова, мы можем получить статистические
свойства коэффициентов
![]() , соответствующих
атмосферным фазовым аберрациям. Математические
преобразования приводят к простой формуле:
, соответствующих
атмосферным фазовым аберрациям. Математические
преобразования приводят к простой формуле:
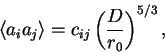 |
(16) |
где коэффициенты ![]() -
элемены так называемой матрицы Нолля.
Коэффициенты нижних порядков (до радиального
-
элемены так называемой матрицы Нолля.
Коэффициенты нижних порядков (до радиального
порядка 3) даны в таблице.
| i \ j | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0.449 | 0 | 0 | 0 | 0 | 0 | 0.0142 | 0 | 0 |
| 3 | 0 | 0.449 | 0 | 0 | 0 | 0.0142 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0.0142 | 0 | 0 | 0 | 0.00619 | 0 | 0 | 0 |
| 8 | 0.0142 | 0 | 0 | 0 | 0 | 0 | 0.00619 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00619 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00619 |
Как можно видеть, матрица Нолля почти
диагональна (не для слишком больших порядков,
однако). Почему пропущен
коэффициент ![]() ? Для модели турбулентности Колмогорова он
бесконечен! Однако, первая (поршневая) мода
? Для модели турбулентности Колмогорова он
бесконечен! Однако, первая (поршневая) мода
для построения изображения не нужна.
Вопрос: Для 4-х-метрового
телескопа и качестве изображения 1 угловую секунду вычислите
среднее квадратическое значение
амплитуды наклона в радианах( для длины волны 0.5
мкм.) Преобразуйте это в среднеквадратическую
амплитуду
движения звездного изображения. Эта амплитуда
зависит от длины волны?
Что случится, если мы исправим первые моды с
помощью адаптивной оптики? Соответствующие
коэффициенты
станут равны нулю и общая фазовая вариация
уменьшится. Обозначая усредненную по зрачку
фазовую вариацию как ![]() , мы запишем:
, мы запишем:
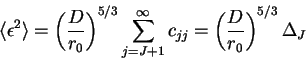 |
(17) |
где первые ![]() мод Цернике скорректированы.
мод Цернике скорректированы.
В целом, неисправленная фазовая вариация (все
моды, исключая поршневую) соответствуют ![]() . Другими словами, в
телескопе с диаметром апертуры
. Другими словами, в
телескопе с диаметром апертуры ![]() атмосферная фазовая вариация около одного
атмосферная фазовая вариация около одного
квадратного радиана. Если скорректированы
наклоны, то ![]() .
Это означает, что наклоны
.
Это означает, что наклоны
составляют 87% полной фазовой вариации.
Скорректировав моды до радиального порядка 2
останется![]() , радиальный порядок 3 оставит
нескорректированную вариацию
, радиальный порядок 3 оставит
нескорректированную вариацию![]() . Как видите, дальнейшее
уменьшение
. Как видите, дальнейшее
уменьшение
фазовой вариации требует исправления всё
большего и большего числа мод Цернике.
Для больших номеров корректируемых мод ![]() (
(![]() ,
как бывает в реальных системах) существует
,
как бывает в реальных системах) существует
очень полезная асимптотическая формула Нолля:
| (18) |
Вопрос: Используя значенияf ![]() и
и ![]() ,данные ранее, вычислите
,данные ранее, вычислите ![]() .
.
Сколько мод нужно скорректировать? Оптики
знают, что когда остаточная фаза меньше 1 радиана,
качество
изображения приближается к дифракционному
пределу. Сейчас мы имеем все средства, чтобы
предсказать
требуемое число мод в зависимости от диаметра
телескопа, качестве изображения и длины волны! Для этого
достаточно
записать![]() и обратить все формулы (попытайтесь сделать
это!). Результат таков:
и обратить все формулы (попытайтесь сделать
это!). Результат таков:
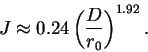 |
(19) |
Вопрос: Сколько мод Цернике
должны быть скорректированы на 4-х-метровом
телескопе для построения изображения
на длинах волн 0.5 и 2.2. мкм при качестве изображения 1 угловая
секунда?
Необходимо ли корректировать турбулентность,
используя моды Цернике? Конечно, нет. Фазовые
аберрации могут
быть измерены и скорректированы с помощью любой
другой системы базисных функций или вообще без
них, работая
непосредственно с самим волновым фронтом.
Оказывается, что моды Цернике - второй по качеству
выбор базисных
функций (лучше всего набор мод, называемых модами
Карунен-Лоэва). Выбор зависит от числа
управляемых параметров
(мод) необходимых для достижения данной степени
коррекции, для мод Цернике их меньше, чем для
локального
управления по волновому фронту.
Резюме: В данной главе дан обзор
основ построения изображения в идеальном и
реальном телескопах (ФРТ ,
ОПФ,
дифракционный предел, коэффициент Штреля). Затем
введены основные параметры атмосферы,
существенные
для адаптивной оптики (структурная фазовая
функция, качество изображения , ![]() , постоянная времени и угол
изопланатизма).
, постоянная времени и угол
изопланатизма).
Рассмотрено разложение случайных фазовых
аберраций по модам Цернике. Теперь мы можем
предсказывать число мод,
которые должны быть скорректированы.
Назад: Введение
Далее: Деформируемые зеркала